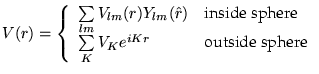
The Full Potential APW methods
The development of the Augmented Plane Wave (APW) methods from Slater's APW, to LAPW and the new APW+lo was described by Schwarz et al. 2001.
A very recent extensive overview is given in:
WIEN2k: An APW+lo program for calculating the properties of solids.
P. Blaha, K.Schwarz, F. Tran, R. Laskowski, G.K.H. Madsen and L.D. Marks,
J. Chem. Phys. 152, 074101 (2020)
The LAPW method
The linearized augmented plane wave (LAPW) method is among the most accurate methods for performing electronic structure calculations for crystals. It is based on the density functional theory for the treatment of exchange and correlation and uses e.g. the local spin density approximation (LSDA). Several forms of LSDA potentials exist in the literature , but recent improvements using the generalized gradient approximation (GGA) are available too. For valence states relativistic effects can be included either in a scalar relativistic treatment (Koelling and Harmon 77) or with the second variational method including spin-orbit coupling (Macdonald 80, Novak 97). Core states are treated fully relativistically (Desclaux 69).
A description of this method to linearize Slater's old APW method (i.e. the LAPW formalism) and further programming hints are found in many references: Andersen 73, 75, Koelling 72, Koelling and Arbman 75, Wimmer et al. 81, Weinert 81, Weinert et al. 82, Blaha and Schwarz 83, Blaha et al. 85, Wei et al. 85, Mattheiss and Hamann 86, Jansen and Freeman 84, Schwarz and Blaha 96). An excellent book by D. Singh (Singh 94) describes all the details of the LAPW method and is highly recommended to the interested reader. Here only the basic ideas are summarized; details are left to those references.
Like most ``energy-band methods``, the LAPW method is a procedure for solving the Kohn-Sham equations for the ground state density, total energy, and (Kohn-Sham) eigenvalues (energy bands) of a many-electron system (here a crystal) by introducing a basis set which is especially adapted to the problem.
This adaptation is achieved by dividing the unit cell into (I) non-overlapping atomic spheres (centered at the atomic sites) and (II) an interstitial region. In the two types of regions different basis sets are used:
- (I) inside atomic sphere t of radius Rt a
linear combination of radial functions times spherical harmonics
Ylm(r) is used (we omit the index t when it is
clear from the context)
where ul(r,El) is the (at the origin) regular solution of the radial Schroedinger equation for energy El (chosen normally at the center of the corresponding band with l-like character) and the spherical part of the potential inside sphere t
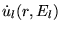 is the energy derivative of ul
taken at the same energy El.
A linear combination of these two functions
constitute the linearization of the radial function; the
coefficients
Alm
and
Blm
are functions of kn
(see
below) determined by requiring that this basis function matches (in
value and slope) the corresponding basis function of the
interstitial region;
is the energy derivative of ul
taken at the same energy El.
A linear combination of these two functions
constitute the linearization of the radial function; the
coefficients
Alm
and
Blm
are functions of kn
(see
below) determined by requiring that this basis function matches (in
value and slope) the corresponding basis function of the
interstitial region; 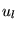 and
and 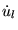 are obtained by numerical
integration of the radial Schroedinger equation on a radial mesh
inside the sphere.
are obtained by numerical
integration of the radial Schroedinger equation on a radial mesh
inside the sphere.
- (II) in the interstitial region a plane wave expansion is used
where kn=k+Kn; Kn are the reciprocal lattice vectors and k is the wave vector inside the first Brillouin zone. Each plane wave is augmented by an atomic-like function in every atomic sphere.
- Abt R., Ambrosch-Draxl C. and Knoll P. 1994 Physica B 194-196
- Abt R. 1997 PhD Theses, Univ.Graz
- Andersen O.K. 1973 Solid State Commun. 13, 133
- -- 1975 Phys. Rev. B 12, 3060
- Ambrosch-Draxl C., Majewski J. A., Vogl P., and Leising G. 1995, PRB 51 9668
- Blaha P. and Schwarz K. 1983 Int. J. Quantum Chem. XXIII, 1535
- Blaha P., Schwarz K., and Herzig P 1985 Phys. Rev. Lett. 54, 1192
- Blaha P., Schwarz K., Sorantin P.I. and Trickey S.B. 1990 Comp. Phys. Commun. 59, 399
- Blöchl P.E., Jepsen O. and Andersen O.K. 1994, Phys. Rev B 49, 16223
- Desclaux J.P. 1969 Comp. Phys. Commun. 1, 216; note that the
actual code we use is an apparently unpublished relativistic
version of the non-relativistic code described in this paper.
Though this code is widely circulated, we have been unable to
find a formal reference for it.
- -- 1975 Comp. Phys. Commun. 9, 31; this paper contains much
of the Dirac-Fock treatment used in Desclaux's relativistic LSDA
code.
- Jansen H.J.F. and Freeman A.J. 1984 Phys. Rev. B 30, 561
- -- 1986 Phys. Rev. B 33, 8629
- Koelling D.D. 1972 J. Phys. Chem. Solids 33, 1335
- Koelling D.D. and Arbman G.O. 1975 J.Phys. F: Met. Phys. 5, 2041
- Koelling D.D. and Harmon B.N. 1977 J. Phys. C: Sol. St. Phys. 10, 3107
- Kohler B., Wilke S., Scheffler M., Kouba R. and Ambrosch-Draxl C. 1996
Comp.Phys.Commun. 94, 31
- Krimmel H.G., Ehmann J., Elsässer C., Fähnle M. and
Soler J.M. 1994, Phys.Rev. B50, 8846
- Kuneš J, Novák P., Schmid R., Blaha P. and Schwarz K. 2001, Phys. Rev. B64, 153102
- MacDonald A. H., Pickett, W. E. and Koelling, D. D. 1980 J. Phys. C 13, 2675
- Madsen G. K. H., Blaha P, Schwarz K, Sjöstedt E and Nordström L 2001, Phys. Rev. B
- Mattheiss L.F. and Hamann D.R. 1986 Phys. Rev. B 33, 823
- Neckel A., Schwarz K., Eibler R. and Rastl P. 1975 Microchim.Acta, Suppl.6, 257
- Novak P. 1997 to be published, see also $WIENROOT/SRC/novak_lecture_on_spinorbit.ps
- Novák P. , Boucher F., Gressier P., Blaha P. and
Schwarz K. 2001 Phys. Rev. B 63, 235114
- Schwarz K. and Blaha P.: Lecture Notes in Chemistry 67, 139 (1996)
- Schwarz K., P.Blaha and Madsen, G. K. H. 2001 Comp.Phys.Commun.
- Singh D. 1991, Phys.Rev. B43, 6388
- Singh D. 1994, Plane waves, pseudopotentials and the LAPW method,
Kluwer Academic
- Sjöstedt E, Nordström L and Singh D. J. 2000 Solid State Commun. 114, 15
- Sofo J and Fuhr J 2001: $WIENROOT/SRC/aim_sofo_notes.ps
- Soler J.M. and Williams A.R. 1989, Phys.Rev. B40, 1560
- Stahn J, Pietsch U, Blaha P and Schwarz K. 2001, Phys.Rev. B63, 165205
- Wei S.H., Krakauer H., and Weinert M. 1985 Phys. Rev. B 32, 7792
- Weinert M. 1981 J. Math. Phys. 22, 2433
- Weinert M., Wimmer E., and Freeman A.J. 1982 Phys. Rev. B26, 4571
- Wimmer E., Krakauer H., Weinert M., and Freeman A.J. 1981
Phys. Rev. B24, 864
- Yu R., Singh D. and Krakauer H. 1991, Phys.Rev. B43, 6411
The solutions to the Kohn-Sham equations are expanded in this combined basis set of LAPW's according to the linear variation method
and the coefficients cn are determined by the Rayleigh-Ritz variational principle. The convergence of this basis set is controlled by a cutoff parameter RmtKmax= 6 - 9, where Rmt is the smallest atomic sphere radius in the unit cell and Kmax is the magnitude of the largest K vector.
In order to improve upon the linearization (i.e. to increase the flexibility of the basis) and to make possible a consistent treatment of semicore and valence states in one energy window (to ensure orthogonality) additional (kn independent) basis functions can be added. They are called "local orbitals" (Singh 91) and consist of a linear combination of 2 radial functions at 2 different energies (e.g. at the 3s and 4s energy) and one energy derivative (at one of these energies):
The coefficients
Alm,
Blm, and
Clm,
are determined by
the requirements that ![]() should be normalized and has zero value
and slope at the sphere boundary.
should be normalized and has zero value
and slope at the sphere boundary.
The APW+lo method
Sjöstedt, Nordström and Singh (2000) have shown that the standard LAPW method with the additional constraint on the PWs of matching in value AND slope to the solution inside the sphere is not the most efficient way to linearize Slater's APW method. It can be made much more efficient when one uses the standard APW basis, but of course with ul(r,El) at a fixed energy El in order to keep the linear eigenvalue problem. One then adds a new local orbital (lo) to have enough variational flexibility in the radial basisfunctions:
Thus we construct basis functions that have ``kinks'' at the sphere boundary, which makes it necessary to include surface terms in the kinetic energy part of the Hamiltonian. Note, however, that the total wavefunction is of course smooth and differentiable.
As shown by Madsen et al. (2001) this new scheme converges practically to identical results as the LAPW method, but allows to reduce ``RKmax'' by about one, leading to significantly smaller basis sets (up to 50 %) and thus the corresponding the computational time is drastically reduced (up to an order of magnitude). Within one calculation a mixed ``LAPW and APW+lo'' basis can be used for different atoms and even different l-values for the same atom (Madsen et al. 2001). In general one describes by APW+lo those orbitals which converge most slowly with the number of PWs (such as TM 3d states) or the atoms with a small sphere size, but the rest with ordinary LAPWs. One can also add a second ``lo'' at a different energy so that both, semicore and valence states, can be described simultaneously.
General considerations
In its general form the LAPW method expands the potential in the following form
and the charge densities analogously. Thus no shape approximations are made, a procedure frequently called the ``full-potential`` method.
The ``muffin-tin`` approximation used in early band calculations corresponds to retaining only the L=0 and M=0 component in the first expression of equ. (9) and only the K=0 component in the second. This (much older) procedure corresponds to taking the spherical average inside the spheres and the volume average in the interstitial region.
The total energy is computed according to Weinert et al. 82.
Rydberg atomic units are used except internally in the atomic-like programs (LSTART and LCORE) or in subroutine outwin (LAPW1, LAPW2), where Hartree units are used. The output is always given in Rydberg units.
The forces at the atoms are calculated according to Yu et al (91). For the implementation of this formalism in WIEN see Kohler et al (94) and Madsen et al. 2001. An alternative formulation by Soler and Williams (89) has also been tested and found to be equivalent, both in computationally efficiency and numerical accuracy and the respective code is available from M.Fähnle (Krimmel et al 94).
The Fermi energy and the weights of each band state can be calculated using a modified tetrahedron method (Bloechl et al. 94), a Gaussian or a temperature broadening scheme.
Spin-orbit interactions can be considered via a second variational step using the scalar-relativistic eigenfunctions as basis. (See MacDonald 80, Singh 94 and Novak 97). In order to overcome the problems due to the missing p1/2 radial basis function in the scalar-relativistic basis (which corresponds to p3/2, we have recently extended the standard LAPW basis by an additional p1/2-local orbital'', i.e. a LO with a p1/2 basis function, which is added in the second-variational SO calculation (Kunes et al. 2001).
It is well known that for localized electrons (like the 4f states in lanthanides or 3d states in some TM-oxides) the LDA (GGA) method is not accurate enough for a proper description. Thus we have implemented various forms of the LDA+U method as well as the ``Orbital polarization method'' (OP) (see Novak 2001 and references therein).
One can also consider interactions with an external magnetic (see Novak 2001) or electric field (via a supercell approach, see Stahn et al. 2000).
PROPERTIES:
The density of states (DOS) can be calculated using the modified tetrahedron method of Blöchl et al. 94.
X-ray absorption and emission spectra are determined using Fermi's golden rule and dipole matrix elements (between a core and valence or conduction band state respectively). (Neckel et al. 75)
X-ray structure factors are obtained by Fourier Transformation of the charge density.
Optical properties are obtained using the ``Joint density of states'' modified with the respective dipole matrix elements according to Ambrosch et al. 95, Abt et al. 94, Abt 97. A Kramers-Kronig transformation is also possible.
An analysis of the electron density according to Bader's ``atoms in molecules'' theory can be made using a program by J. Sofo and J. Fuhr (2001)
References
©2001 by P. Blaha and K. Schwarz
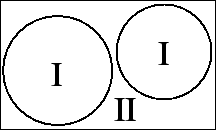
![\begin{displaymath}
\phi_{k_n} = \sum_{lm} [ A_{lm} u_l(r,E_l) +
B_{lm} \dot u_l(r,E_l) ] Y_{lm}(\hat r)
\end{displaymath}](img34.gif)
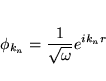
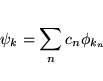
![\begin{displaymath}
\phi_{lm}^{LO} = [ A_{lm} u_l(r,E_{1,l}) + B_{lm} \dot u_l(r,E_{1,l}) +
C_{lm} u_l(r,E_{2,l}) ] Y_{lm} (\hat r)
\end{displaymath}](img59.gif)
![\begin{displaymath}
\phi_{{\bf k}_n} = \sum_{lm} [ A_{lm,{\bf k}_n} u_l(r,E_l) ] Y_{lm}(\hat{\bf r})
\end{displaymath}](img74.png)
![\begin{displaymath}
\phi_{lm}^{lo} = [ A_{lm} u_l(r,E_{1,l}) + B_{lm} \dot u_l(r,E_{1,l})
] Y_{lm} (\hat{\bf r})
\end{displaymath}](img75.png)